Số hữu tỉ là gì?
Trong hành trình khám phá thế giới số học, một trong những khái niệm căn bản mà học sinh trung học cơ sở cần nắm vững là số hữu tỉ là gì. Đây là nền tảng để hiểu rõ cấu trúc của tập hợp số thực, từ đó mở rộng kiến thức sang đại số và giải tích. Tuy nhiên, không phải ai cũng hiểu đầy đủ về số hữu tỉ, cách phân biệt với số thực hay cách biểu diễn chúng trên trục số.
Hãy cùng tìm hiểu chi tiết từ định nghĩa, biểu diễn, mối liên hệ với các tập số khác cho đến cách nhận biết một số có phải là số hữu tỉ hay không qua bài viết dưới đây.
Số hữu tỉ là gì?
Số hữu tỉ là những số có thể biểu diễn được dưới dạng phân số a/b, trong đó:
a và b là số nguyên (a, b ∈ ℤ),
b ≠ 0.
Hay nói cách khác, số hữu tỉ là số có thể viết được dưới dạng thương của hai số nguyên mà mẫu khác 0.
Ký hiệu
Tập hợp các số hữu tỉ được ký hiệu là ℚ, lấy từ chữ “Quotient” trong tiếng Anh, nghĩa là thương số.
Những số không phải là số hữu tỉ:
√2, π, e, 0.1010010001…
→ Đây là các số không thể viết dưới dạng phân số hữu hạn → số vô tỉ.
Biểu diễn số hữu tỉ là gì trên trục số
Số hữu tỉ là tập con của số thực, vì thế hoàn toàn có thể biểu diễn được trên trục số.
Cách biểu diễn số hữu tỉ
Với số nguyên hoặc phân số đơn giản:
Ví dụ: 1/2 nằm giữa 0 và 1, ở chính giữa.
-3 nằm bên trái gốc tọa độ, cách 0 ba đơn vị.
Với phân số không đơn giản:
Ví dụ: 3/4 nằm giữa 0.5 và 1.
7/2 = 3.5 → nằm giữa 3 và 4.
Số thập phân vô hạn tuần hoàn:
Dùng giá trị gần đúng để xác định vị trí gần đúng.
Ví dụ: 0.666… ≈ 2/3 → nằm giữa 0.6 và 0.7.
Cách chia trục số:
Chia đoạn đơn vị thành các phần nhỏ tương ứng mẫu số.
Ví dụ: biểu diễn 3/5 → chia đoạn 0–1 thành 5 phần, lấy điểm thứ ba.
Mẹo:
Đổi số hữu tỉ là gì về dạng thập phân (nếu cần) để xác định vị trí dễ hơn.
Có thể vẽ phác để hiểu trực quan vị trí của số trên trục.
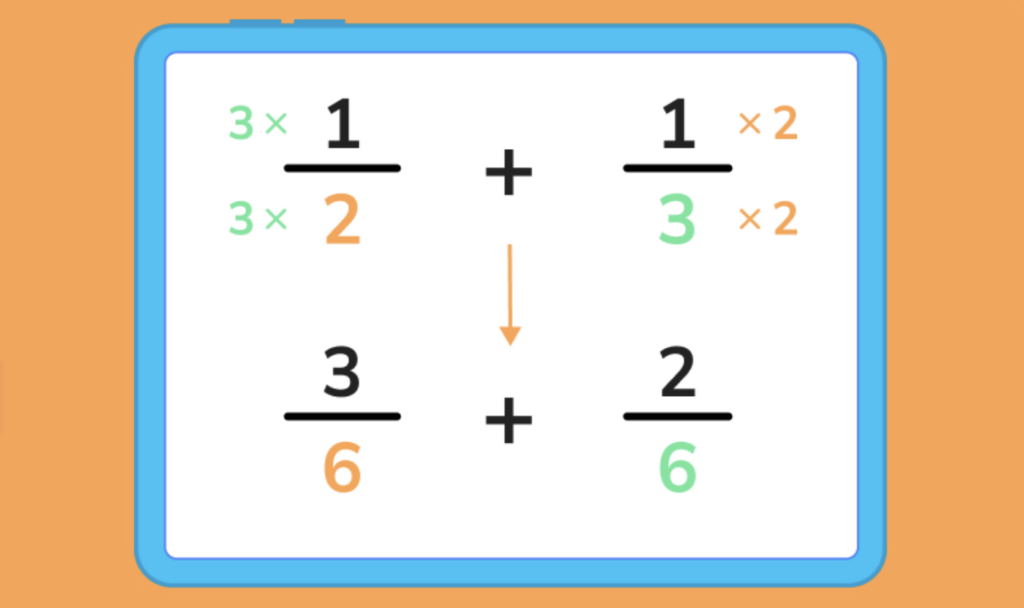Phép cộng số hữu tỉTập hợp số hữu tỉ (ℚ) bao gồm nhiều tập con, trong đó có số nguyên, số thập phân hữu hạn, và số thập phân vô hạn tuần hoàn. Ta có thể hiểu mối quan hệ này như sau:
Số nguyên là số hữu tỉ
Mỗi số nguyên a có thể viết thành a/1
→ Ví dụ: 5 = 5/1, -2 = -2/1
Số thập phân hữu hạn là số hữu tỉ
Có thể chuyển về phân số bằng cách nhân chia.
→ 0.75 = 3/4, 2.1 = 21/10
Số thập phân vô hạn tuần hoàn cũng là số hữu tỉ
Ví dụ:
0.666… = 2/3
1.272727… = 127/99
Không phải tất cả số thập phân đều là số hữu tỉ
Những số thập phân vô hạn không tuần hoàn → là số vô tỉ, ví dụ:
0.1010010001… (không có chu kỳ lặp lại)
Phân biệt số hữu tỉ và số thực
Số hữu tỉ là gì - một phần của tập hợp số thực (ℝ). Tuy nhiên, số thực còn bao gồm cả số vô tỉ.
Học sinh trong giờ toánBảng so sánh:
|
Tiêu chí
|
Số hữu tỉ (ℚ)
|
Số thực (ℝ)
|
|
Định nghĩa
|
Số viết được dưới dạng a/b, a, b ∈ ℤ, b ≠ 0
|
Bao gồm cả số hữu tỉ và vô tỉ
|
|
Thập phân
|
Hữu hạn hoặc vô hạn tuần hoàn
|
Bao gồm mọi số trên trục số
|
|
Ví dụ
|
-3, 1/2, 0.75, 0.333…
|
√2, π, e, 0.1010010001…
|
|
Tính chất
|
Có thể liệt kê được
|
Không thể liệt kê hết
|
Để xác định một số bất kỳ có phải là số hữu tỉ hay không, bạn có thể áp dụng các cách sau:
Kiểm tra dạng phân số
Nếu số đó viết được dưới dạng a/b với a, b nguyên và b ≠ 0 → Là số hữu tỉ.
Ví dụ:
5 = 5/1 → số hữu tỉ
-4/7 → rõ ràng là số hữu tỉ
Số hữu tỉQuan sát phần thập phân
Thập phân hữu hạn → số hữu tỉ
VD: 0.6, 1.25, -3.875
Thập phân vô hạn tuần hoàn → số hữu tỉ
VD: 0.333…, 1.121212…
Thập phân vô hạn không tuần hoàn → không phải số hữu tỉ
VD: 0.1010010001…, √2, π
Dùng định lý toán học (nâng cao)
Sử dụng phép biến đổi đại số để xác minh một số là vô tỉ hay hữu tỉ.
VD: Giả sử √2 là hữu tỉ, chứng minh ngược lại bằng mâu thuẫn.
Dùng máy tính hoặc phần mềm hỗ trợ
Một số phần mềm có thể giúp chuyển thập phân sang phân số để kiểm tra số đó có là hữu tỉ không.
Số hữu tỉ là gì - một khái niệm cốt lõi trong toán học, là nền tảng để xây dựng và mở rộng kiến thức về số thực, đại số và giải tích. Nắm chắc định nghĩa, biết cách biểu diễn trên trục số, hiểu được mối quan hệ giữa số hữu tỉ và các tập hợp số khác sẽ giúp bạn học toán tốt hơn và ứng dụng vào đời sống thực tế hiệu quả hơn.