Dấu hiệu nhận biết hình vuông
Hình vuông là một trong những hình học cơ bản và quen thuộc nhất trong toán học, xuất hiện từ sách giáo khoa đến đời sống hằng ngày. Đây là hình tứ giác đặc biệt, có tất cả các cạnh bằng nhau và các góc đều bằng 90 độ. Hiểu rõ đặc điểm cơ bản của hình vuông giúp học sinh, sinh viên dễ dàng nhận biết, áp dụng vào các bài toán hình học và các tình huống thực tế.
Một số đặc điểm cơ bản của hình vuông:
Các cạnh bằng nhau: Tất cả bốn cạnh của hình vuông đều bằng nhau. Nếu hình vuông có cạnh dài a, thì:
AB=BC=CD=DA=a
Các góc vuông: Mỗi góc trong hình vuông đều là 90 độ. Điều này giúp hình vuông trở thành tứ giác đều, đồng thời tạo điều kiện thuận lợi cho việc đo đạc, thiết kế và xây dựng.
Đường chéo bằng nhau và vuông góc: Hai đường chéo của hình vuông không chỉ bằng nhau mà còn cắt nhau tại trung điểm của mỗi đường, tạo thành các góc vuông 90 độ. Nếu đường chéo dài d, thì:
d=a√ 2
Tính đối xứng cao: Hình vuông có bốn trục đối xứng và tâm đối xứng nằm tại giao điểm hai đường chéo. Tính đối xứng này giúp hình vuông dễ dàng sử dụng trong thiết kế, trang trí và các bài toán hình học.
Những đặc điểm này giúp hình vuông trở thành hình học cơ bản nhưng cực kỳ quan trọng, được ứng dụng rộng rãi trong học tập, kỹ thuật và đời sống.
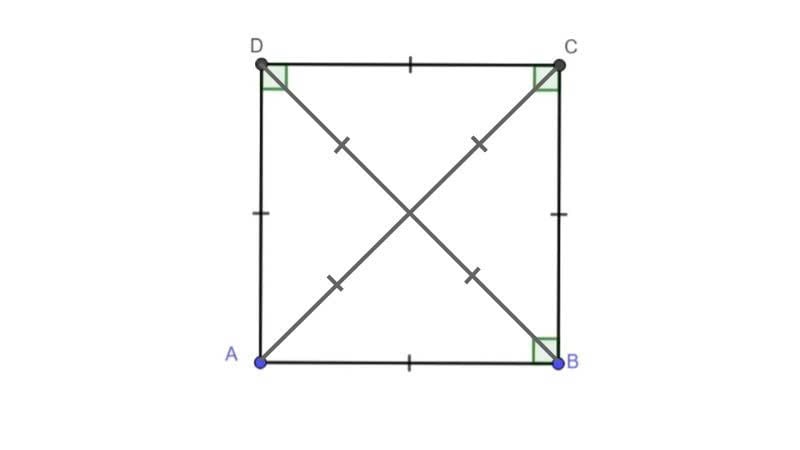
Tính chất hình vuôngĐể nhận biết hình vuông, bạn có thể dựa vào nhiều dấu hiệu cơ bản sau:
Tất cả các cạnh bằng nhau: Nếu tứ giác có bốn cạnh bằng nhau và các góc vuông, chắc chắn đó là hình vuông. Đây là dấu hiệu nhận biết đơn giản nhất.
Các góc đều vuông: Nếu tứ giác có bốn góc 90 độ và hai đường chéo bằng nhau, tứ giác đó là hình vuông.
Đường chéo cắt nhau tại trung điểm và vuông góc: Hai đường chéo của hình vuông luôn bằng nhau, cắt nhau tại trung điểm, tạo thành các góc 90 độ. Đây là dấu hiệu quan trọng để phân biệt hình vuông với hình chữ nhật.
Diện tích và chu vi liên quan: Nếu biết cạnh a, diện tích S=a² , chu vi P=4a. Những dấu hiệu này giúp nhận diện hình vuông qua các phép đo thực tế.
So sánh với các tứ giác khác:
Hình chữ nhật: Các cạnh đối bằng nhau nhưng các cạnh kề không bằng nhau.
Hình thoi: Các cạnh bằng nhau nhưng góc không phải 90 độ.
Hình bình hành: Các cạnh đối bằng nhau, góc không phải 90 độ.
Hiểu các dấu hiệu này giúp học sinh dễ dàng phân biệt hình vuông trong các bài tập hình học, bài toán thực hành, và các tình huống đo đạc thực tế.

Hình vuông minh họaHình vuông không chỉ là khái niệm lý thuyết mà còn có ứng dụng đa dạng trong học tập và đời sống thực tế.
Trong học tập
Bài tập toán học: Hình vuông xuất hiện nhiều trong các bài toán về diện tích, chu vi, đường chéo, hình học phẳng và không gian.
Hình học giải tích: Hình vuông giúp học sinh hiểu về tọa độ, đồ thị, phép đối xứng, các phép biến hình như tịnh tiến, quay, phản chiếu.
Rèn luyện tư duy logic: Việc nhận biết hình vuông từ các dấu hiệu hình học giúp học sinh phát triển khả năng quan sát, phân tích và suy luận logic.
Trong đời sống
Thiết kế kiến trúc: Hình vuông thường xuất hiện trong thiết kế phòng, cửa sổ, bàn ghế, gạch lát sàn. Hình vuông giúp không gian cân đối, tạo thẩm mỹ và thuận tiện khi sắp xếp.
Ví dụ: Các tấm gạch lát sàn có hình vuông giúp lát đều và dễ đo đạc. Nếu mỗi viên gạch cạnh a, diện tích của viên gạch là a² .
Trang trí và mỹ thuật: Hình vuông được sử dụng trong hoa văn, họa tiết trang trí, tranh vẽ, thiết kế logo. Tính đối xứng cao của hình vuông tạo sự cân bằng và hài hòa.
Kỹ thuật và đo lường: Trong kỹ thuật, hình vuông xuất hiện trong các chi tiết cơ khí, bảng mạch, linh kiện. Việc nhận biết hình vuông giúp kỹ sư đo lường chính xác, bố trí các chi tiết đồng đều.
Đời sống hàng ngày: Nhiều vật dụng như bàn, khay, nắp hộp, đồng hồ… đều có hình vuông. Nhận biết hình vuông giúp chọn lựa vật dụng phù hợp với không gian và nhu cầu sử dụng.
Trong giáo dục và giải trí
Trò chơi học tập: Hình vuông được dùng trong các trò chơi logic, xếp hình, ghép tranh, giúp trẻ rèn luyện tư duy và nhận biết hình học.
Các ứng dụng phần mềm: Trong thiết kế đồ họa, lập trình, hình vuông xuất hiện dưới dạng pixel, khung vẽ, biểu tượng, giúp người dùng bố trí hình ảnh chính xác.
Ứng dụng rộng rãi này chứng minh rằng hình vuông không chỉ là hình học cơ bản mà còn là yếu tố thiết yếu trong nhiều lĩnh vực của đời sống.

Học sinh trong giờKhi nhận biết hình vuông, cần lưu ý một số điểm để tránh nhầm lẫn với các tứ giác khác:
Không nhầm với hình chữ nhật: Hình chữ nhật có bốn góc vuông nhưng các cạnh kề không bằng nhau. Kiểm tra các cạnh bằng nhau để xác định hình vuông.
Không nhầm với hình thoi: Hình thoi có bốn cạnh bằng nhau nhưng các góc không phải 90 độ. Đo góc để phân biệt.
Kiểm tra đường chéo: Hai đường chéo hình vuông bằng nhau, cắt nhau tại trung điểm và vuông góc. Đây là dấu hiệu nhận biết hình vuông quan trọng để nhận biết chính xác.
Sử dụng công cụ đo lường: Khi đo thực tế, sử dụng thước đo cạnh, thước đo góc hoặc compa để kiểm tra.
Áp dụng công thức:
Chu vi P=4 * a
Diện tích S=a²
Đường chéo d=a√ 2
Những công thức này giúp xác định hình vuông một cách nhanh chóng và chính xác.
Lưu ý các điểm này giúp học sinh, kỹ sư, nhà thiết kế và bất kỳ ai cần đo đạc nhận biết hình vuông mà không bị nhầm lẫn.
Hình vuông là một tứ giác đặc biệt, có bốn cạnh bằng nhau, bốn góc vuông và đường chéo vuông góc bằng nhau. Dấu hiệu nhận biết hình vuông dựa vào các cạnh bằng nhau, góc vuông, đường chéo bằng nhau và tính đối xứng.
Hình vuông có ứng dụng đa dạng trong học tập, đời sống, kiến trúc, kỹ thuật và thiết kế mỹ thuật. Nhận biết chính xác hình vuông giúp đo lường, thiết kế, sắp xếp vật dụng và giải bài toán hình học hiệu quả.
Khi nhận biết hình vuông, cần lưu ý không nhầm lẫn với hình chữ nhật, hình thoi, kiểm tra đường chéo và sử dụng công cụ đo lường khi cần. Áp dụng các công thức về chu vi, diện tích và đường chéo giúp xác định hình vuông chính xác.
Hình vuông là một hình học cơ bản nhưng cực kỳ quan trọng, có tính ứng dụng cao và xuất hiện trong nhiều lĩnh vực của đời sống hiện đại. Hiểu và dấu hiệu nhận biết hình vuông giúp nâng cao tư duy logic, kỹ năng đo lường và khả năng thiết kế.