Điểm đối xứng là gì?
Trong hình học, điểm đối xứng là gì khái niệm cơ bản nhưng vô cùng quan trọng, xuất hiện trong nhiều bài toán về hình học phẳng, không gian, và ứng dụng thực tế. Điểm đối xứng giúp xác định vị trí cân bằng của các hình, phân tích tính chất hình học, cũng như phát triển tư duy logic và hình học không gian.
Về bản chất, điểm đối xứng của một hình là điểm mà khi quay hoặc phản chiếu hình qua điểm đó, hình vẫn trùng với chính nó. Nói cách khác, điểm đối xứng là trung tâm của sự cân bằng giữa các phần của hình.
Ví dụ minh họa:
Hình vuông có một điểm đối xứng là giao điểm hai đường chéo. Khi quay hình vuông 180° quanh điểm này, hình vẫn trùng với vị trí ban đầu.
Hình chữ nhật cũng có điểm đối xứng là giao điểm hai đường chéo.
Một đoạn thẳng AB có trung điểm M là điểm đối xứng của đoạn thẳng này, bởi A và B cân xứng qua M.
Hiểu rõ khái niệm điểm đối xứng giúp học sinh và người học dễ dàng nhận diện tính chất cân xứng trong hình học, đồng thời áp dụng vào các bài toán về phản xạ, quay, và biến đổi hình học.
Học sinh trong giờ
Để nhận biết một điểm là điểm đối xứng, có thể dựa vào một số dấu hiệu cơ bản sau:
Các đoạn thẳng cân xứng qua điểm: Nếu điểm M là điểm đối xứng, thì với mọi điểm A trên hình, tồn tại một điểm B sao cho M là trung điểm của đoạn AB.
Đường chéo giao nhau: Trong các đa giác đều như hình vuông, hình chữ nhật, hình thoi, giao điểm các đường chéo thường là điểm đối xứng.
Tính chất quay 180° : Điểm đối xứng là tâm của phép quay 180° mà hình quay qua vẫn trùng với vị trí ban đầu.
Sự cân xứng đều: Hình có thể được chia thành hai nửa đối xứng nhau qua điểm đối xứng.
Ví dụ cụ thể:
Hình vuông ABCD có giao điểm O của hai đường chéo AC và BD. O là điểm đối xứng, bởi AO=OC, BO=OD.
Đoạn thẳng AB có trung điểm M. M là điểm đối xứng của A và B. Khi quay đoạn thẳng 180° quanh M, đoạn thẳng vẫn trùng với chính nó.
Nhận biết các dấu hiệu này giúp học sinh áp dụng chính xác trong bài tập hình học, vẽ hình, và giải các bài toán về đối xứng trục và đối xứng tâm.
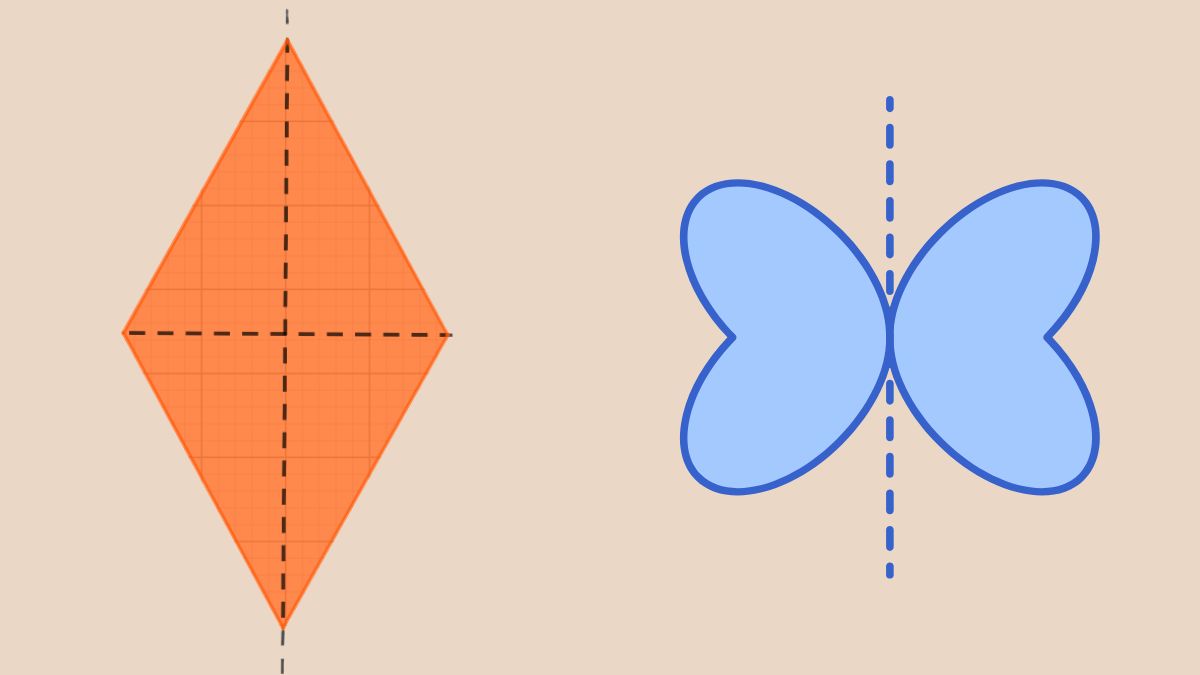Trục đối xứngViệc xác định điểm đối xứng không quá phức tạp, nhưng cần dựa vào tọa độ hoặc tính chất hình học.
Điểm đối xứng của một đoạn thẳng
Nếu đoạn thẳng có hai điểm A(x₁, y₁) và B(x₂, y₂), trung điểm M(xm, ym) là điểm đối xứng của hai điểm A và B. Công thức:
xm=(x₁ + x₂) / 2
ym=(y₁ + y₂) / 2
Ví dụ: A(2, 3), B(6, 7)
xm=(2 + 6) / 2=4
ym=(3 + 7) / 2=5
M(4, 5) là điểm đối xứng
Điểm đối xứng trong đa giác
Hình vuông: Điểm giao nhau hai đường chéo là điểm đối xứng. Nếu tọa độ các đỉnh là A(x₁, y₁), B(x₂, y₂), C(x₃, y₃), D(x₄, y₄), điểm đối xứng O:
Ox=(x₁ + x₃) / 2=(x₂ + x₄) / 2
Oy=(y₁ + y₃) / 2=(y₂ + y₄) / 2
Hình chữ nhật: Tương tự, giao điểm hai đường chéo là điểm đối xứng.
Hình thoi: Điểm giao hai đường chéo cũng là điểm đối xứng.
Xác định điểm đối xứng qua trục tọa độ
Trong hệ tọa độ:
Nếu A(x, y) là một điểm, điểm đối xứng qua gốc tọa độ O(0, 0) là A' (-x, -y).
Nếu điểm đối xứng qua trục Ox: A' (x, -y)
Nếu điểm đối xứng qua trục Oy: A' (-x, y)
Công thức này giúp xác định nhanh điểm đối xứng trong các bài toán vẽ hình, phản xạ, quay hoặc trong các phép biến hình học phẳng.
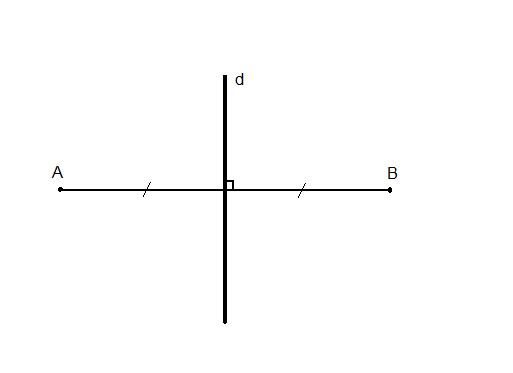Trục đối xứngĐiểm đối xứng không chỉ là khái niệm học tập mà còn có ứng dụng thực tế rộng rãi:
Trong học tập
Bài tập hình học: Điểm đối xứng giúp giải các bài toán đa giác, tính diện tích, xác định trung điểm, vẽ hình cân xứng.
Tư duy hình học: Phân tích điểm đối xứng giúp học sinh phát triển khả năng tưởng tượng không gian, nhận biết trục và tâm đối xứng, áp dụng vào các bài toán phức tạp.
Thiết kế bài vẽ và mô hình: Điểm đối xứng là cơ sở để vẽ hình học cân xứng, thiết kế mô hình, áp dụng trong môn mỹ thuật hoặc kỹ thuật.
Trong đời sống và kỹ thuật
Kiến trúc và thiết kế: Điểm đối xứng được sử dụng trong bố trí nhà cửa, cầu cống, các tòa nhà, giúp cân đối và hài hòa về mặt hình học.
Mỹ thuật và trang trí: Hình ảnh, hoa văn, họa tiết trang trí thường dựa trên điểm đối xứng để tạo sự cân bằng và hài hòa.
Cơ khí và kỹ thuật: Điểm đối xứng giúp xác định trung tâm, cân bằng chi tiết máy, bánh răng, trục quay và các thiết bị cơ khí.
Trong khoa học và công nghệ
Hình học không gian: Điểm đối xứng dùng để xác định tâm quay, tâm đối xứng trong các hình khối, phân tích hình học không gian.
Thiết kế đồ họa và lập trình: Điểm đối xứng giúp vẽ hình, thiết kế icon, bố cục trong các phần mềm đồ họa và lập trình giao diện.
Ứng dụng trong vật lý: Trong vật lý quang học, điểm đối xứng giúp phân tích tia sáng phản xạ, hội tụ và thiết kế hệ quang học.
Trong giáo dục trẻ em
Trò chơi học tập: Điểm đối xứng giúp trẻ nhận biết hình dạng, phát triển tư duy logic, sắp xếp các hình khối cân đối.
Xếp hình và ghép tranh: Điểm đối xứng là cơ sở để trẻ học cách cân bằng các mảnh ghép, nhận biết phần đối xứng và hoàn thiện bức tranh.
Những ứng dụng này chứng minh rằng điểm đối xứng không chỉ là lý thuyết mà còn có giá trị thực tiễn cao trong nhiều lĩnh vực.
Điểm đối xứng trong hình học là điểm trung tâm của sự cân bằng, giúp các phần của hình trùng khớp khi quay 180° hoặc phản chiếu. Nhận biết điểm đối xứng dựa vào các dấu hiệu như trung điểm của đoạn thẳng, giao điểm đường chéo, tính chất quay 180° và cân xứng đều.
Công thức xác định điểm đối xứng là gì:
Trung điểm đoạn thẳng:
xm=(x₁ + x₂) / 2
ym=(y₁ + y₂) / 2
Điểm đối xứng qua gốc tọa độ: A(x, y) → A' (-x, -y)
Điểm đối xứng trong đa giác: giao điểm các đường chéo
Điểm đối xứng có ứng dụng rộng rãi trong học tập, đời sống, kiến trúc, mỹ thuật, kỹ thuật, khoa học và giáo dục trẻ em. Hiểu rõ khái niệm và cách xác định điểm đối xứng giúp học sinh phát triển tư duy hình học, áp dụng vào các bài toán, thiết kế và phân tích hình học thực tế.
Điểm đối xứng là một công cụ mạnh mẽ, vừa đơn giản, vừa ứng dụng đa dạng, giúp cân bằng hình học, thiết kế hình ảnh, tối ưu hóa kỹ thuật và nâng cao khả năng quan sát, tư duy logic trong nhiều lĩnh vực.