Tính đường kính hình tròn
Đường kính là một trong những yếu tố quan trọng nhất khi nghiên cứu về hình tròn. Đường kính của hình tròn được định nghĩa là đoạn thẳng đi qua tâm của hình tròn và nối hai điểm nằm trên chu vi của hình tròn đó. Nói cách khác, đường kính là đoạn thẳng dài nhất có thể vẽ trong một hình tròn.
Đường kính thường được ký hiệu là D và có mối quan hệ trực tiếp với bán kính (r), đó là khoảng cách từ tâm hình tròn đến bất kỳ điểm nào trên chu vi. Cụ thể, công thức đơn giản là:
D=2 × r
Điều này có nghĩa là đường kính luôn gấp đôi bán kính.
Ngoài ra, đường kính còn liên quan chặt chẽ đến chu vi (C) và diện tích (S) của hình tròn. Khi biết chu vi, đường kính được tính bằng công thức:
D=C ÷ π
Và khi biết diện tích, đường kính được tính bằng:
D=2 × √ (S ÷ π)
Hiểu rõ khái niệm về đường kính không chỉ giúp giải các bài toán hình học mà còn rất hữu ích trong đời sống thực tế, ví dụ như đo kích thước bánh xe, vòng tròn trong xây dựng, hay thiết kế các vật dụng hình tròn.
Một điểm quan trọng nữa là đường kính luôn đi qua tâm, vì vậy nếu bạn biết một đường kính, bạn cũng xác định được tâm của hình tròn. Đây là kiến thức cơ bản nhưng cực kỳ quan trọng, vì nó là nền tảng để tính toán các yếu tố khác như chu vi, diện tích, và các ứng dụng trong khoa học, kỹ thuật hay đời sống hàng ngày.
Khái niệm cơ bản về đường kính hình tròn Tính đường kính từ bán kính
Nếu biết bán kính (r) của hình tròn, công thức tính đường kính là:
D=2 × r
Ví dụ:
Bán kính r=5 cm
Đường kính D=2 × 5=10 cm
Tính đường kính từ chu vi
Nếu biết chu vi (C) của hình tròn, công thức là:
D=C ÷ π
Trong đó:
π ≈ 3.14159
Ví dụ:
Chu vi C=31.4 cm
Đường kính D=31.4 ÷ 3.14159 ≈ 10 cm
Tính đường kính từ diện tích
Nếu biết diện tích (S) của hình tròn, công thức là:
D=2 × √ (S ÷ π)
Ví dụ:
Diện tích S=78.5 cm²
Đường kính D=2 × √ (78.5 ÷ 3.14159) ≈ 10 cm
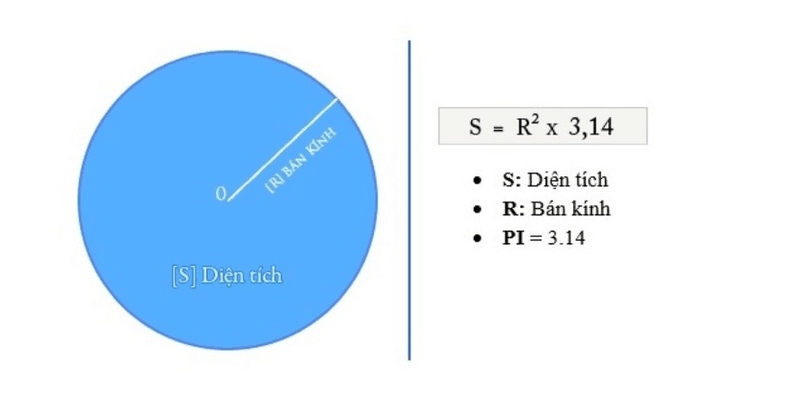
Công thức tính đường kính của hình trònDạng 1: Tính đường kính khi biết bán kính
Bài tập 1: Cho hình tròn có bán kính r=7r=7r=7 cm. Tính đường kính của hình tròn.
Lời giải:
Công thức:D=2 × r
Thay số: D=2 × 7=14 cm
Đáp án: D=14 cm
Dạng 2: Tính đường kính khi biết chu vi
Bài tập 2: Một hình tròn có chu vi C=31.4C=31.4C=31.4 cm. Tính đường kính.
Lời giải:
Công thức:D=C ÷ π
Thay số: D=31.4 ÷ 3.14159 ≈ 10 cm
Đáp án: D ≈ 10 cm
Dạng 3: Tính đường kính khi biết diện tích
Bài tập 3: Cho hình tròn có diện tích S=50.24S=50.24S=50.24 cm² . Tính đường kính.
Lời giải:
Công thức: D=2 × √ (S ÷ π)
Thay số: D=2 × √ (50.24 ÷ 3.14159) ≈ 2 × √ 16 ≈ 2 × 4=8 cm
Đáp án: D=8 cm
Dạng 4: Tính đường kính khi biết chu vi hoặc diện tích thiếu 1 số
Bài tập 4: Chu vi của một hình tròn bằng 2πr. Nếu chu vi là 62.8 cm, hãy tính đường kính.
Lời giải:
D=C ÷ π
D=62.8 ÷ 3.14159 ≈ 20 cm
Đáp án: D ≈ 20 cm
Dạng 5: Bài tập thực tế
Bài tập 5: Một bánh xe có bán kính là 0, 35 m. Tính đường kính của bánh xe.
Lời giải:
D=2 × r=2 × 0, 35=0, 7 m
Đáp án: D=0, 7 m
Các dạng bài tập về tính đường kính của hình trònĐường kính hình tròn không chỉ là một khái niệm toán học mà còn có nhiều ứng dụng thực tiễn trong đời sống hàng ngày và các lĩnh vực kỹ thuật, xây dựng, thiết kế. Việc hiểu rõ và biết cách tính đường kính giúp con người đo đạc chính xác, thiết kế sản phẩm khoa học và thực hiện các phép tính kỹ thuật hiệu quả.
Trong đo đạc và thiết kế
Khi thiết kế các vật dụng có hình tròn như bàn tròn, bánh xe, ống nước, đồng hồ, đường kính là thông số quan trọng để xác định kích thước tổng thể.
Ví dụ, để sản xuất bánh xe ô tô đúng chuẩn, kỹ sư phải tính chính xác đường kính bánh xe dựa trên bán kính và diện tích tiết diện, đảm bảo an toàn và khả năng vận hành.
Trong xây dựng và kiến trúc
Các công trình có chi tiết hình tròn như cổng vòm, cửa sổ tròn, mái nhà hình vòm đều cần tính đường kính để đảm bảo sự cân đối và thẩm mỹ.
Việc đo đường kính cũng giúp tính toán vật liệu cần sử dụng như lượng kính, gỗ, thép cho các chi tiết tròn.
Trong giáo dục và học tập
Học sinh và sinh viên sử dụng công thức tính đường kính hình tròn để giải các bài toán liên quan đến bán kính, chu vi, diện tích.
Đây là kiến thức cơ bản trong môn hình học, làm nền tảng cho các kiến thức nâng cao hơn về hình học phẳng và hình học không gian.
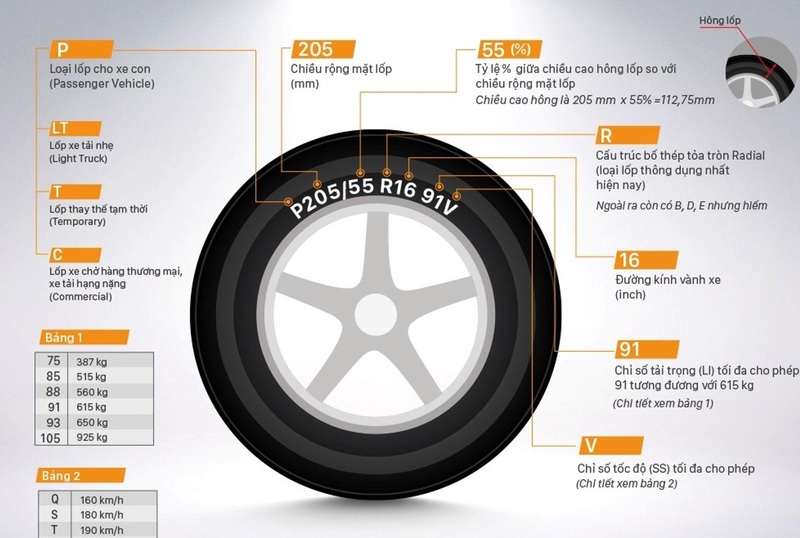
Ứng dụng của đường kính hình tròn trong đời sốngTrong kỹ thuật và sản xuất
Trong các ngành cơ khí, điện tử, sản xuất máy móc, đường kính trục, bánh răng, ổ bi là yếu tố quyết định đến hiệu suất và độ bền của sản phẩm.
Kỹ sư thường phải tính toán chính xác đường kính để lắp ráp các chi tiết tròn với nhau mà không gây hỏng hóc hoặc hao mòn.
Trong đời sống hàng ngày
Đường kính được dùng để đo các vật dụng tròn phổ biến như bát, đĩa, nắp hũ, bánh pizza.
Biết đường kính giúp người dùng lựa chọn sản phẩm phù hợp, tính toán khẩu phần ăn, hoặc thiết kế đồ dùng nhà bếp.
Trong nghệ thuật và trang trí
Trong hội họa, điêu khắc, và trang trí nội thất, các hình tròn thường xuất hiện.
Việc tính đường kính giúp vẽ chính xác các vòng tròn đồng tâm, bố trí hoa văn tròn cân đối và hài hòa.
Việc tính đường kính hình tròn là kiến thức cơ bản nhưng vô cùng quan trọng trong toán học và đời sống hàng ngày. Bằng cách nắm vững các công thức từ bán kính, chu vi hoặc diện tích, bạn có thể dễ dàng giải các bài toán, đo đạc chính xác các vật dụng hình tròn, hay áp dụng trong thiết kế và kỹ thuật. Hiểu rõ khái niệm đường kính không chỉ giúp học sinh, sinh viên học tập hiệu quả mà còn hỗ trợ trong các ứng dụng thực tiễn như xây dựng, sản xuất, và trang trí.
Vì vậy, hãy luyện tập áp dụng công thức tính đường kính trong nhiều tình huống khác nhau để nâng cao kỹ năng toán học và khả năng giải quyết các vấn đề thực tế một cách nhanh chóng và chính xác.>> Tham khảo: Quang hợp là gì