Dấu hiệu nhận biết hình vuông
Hình vuông là một tứ giác đặc biệt có bốn cạnh bằng nhau và bốn góc vuông (90° ). Nói cách khác, hình vuông là hình chữ nhật có bốn cạnh bằng nhau, đồng thời cũng là hình thoi có một góc vuông.
Hình vuông là sự kết hợp hài hòa giữa hình chữ nhật và hình thoi, vì nó vừa có các cạnh bằng nhau, vừa có các góc vuông.
Hình vuông là tứ giác đặc biệt, kết hợp cả tính chất của hình chữ nhật và hình thoi. Dưới đây là các tính chất cơ bản và đặc trưng của hình vuông:
Tính chất về cạnh
Bốn cạnh của hình vuông bằng nhau.
👉 Công thức: AB=BC=CD=DA
Tính chất về góc
Bốn góc của hình vuông đều là góc vuông.
👉 Công thức: ∠ A=∠ B=∠ C=∠ D=90°
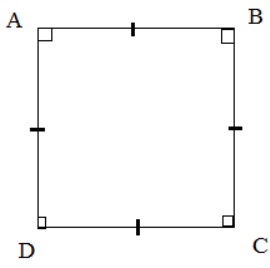
Hình vuông có những tính chất đặc trưng nào?Tính chất về đường chéo
Hai đường chéo bằng nhau: AC=BD
Hai đường chéo vuông góc với nhau: AC ⊥ BD
Hai đường chéo cắt nhau tại trung điểm.
👉 Gọi giao điểm là O thì: AO=BO=CO=DO
Tính chất đối xứng
Hình vuông có 4 trục đối xứng.
Có 1 tâm đối xứng là giao điểm hai đường chéo.
Tính chất về chu vi và diện tích
Chu vi hình vuông:
👉 P=4 × a
(Trong đó: a là độ dài cạnh hình vuông)
Diện tích hình vuông:
👉 S=a²
Một số tính chất đặc biệt khác
Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.
Hình vuông cũng là hình thoi có bốn góc vuông.
Mỗi đường chéo chia hình vuông thành hai tam giác vuông cân bằng nhau.
Trong hình học, hình vuông là một tứ giác đặc biệt, vừa mang tính chất của hình chữ nhật, vừa mang tính chất của hình thoi. Vì vậy, có nhiều dấu hiệu nhận biết hình vuông khác nhau, giúp ta xác định hoặc chứng minh một tứ giác là hình vuông trong các bài toán hình học.
Dưới đây là các dấu hiệu thường gặp nhất:
Hình chữ nhật có hai cạnh kề bằng nhau
Nếu một hình chữ nhật có hai cạnh kề bằng nhau, thì hình đó là hình vuông.
Giải thích: Hình chữ nhật vốn có bốn góc vuông, khi hai cạnh kề bằng nhau thì bốn cạnh sẽ bằng nhau, từ đó hình trở thành hình vuông.
Ví dụ: Trong hình chữ nhật ABCD, nếu có AB=AD, thì hình chữ nhật ABCD chính là hình vuông.

Dấu hiệu để nhận biết hình vuôngHình thoi có một góc vuông
Nếu một hình thoi có một góc vuông, thì hình đó là hình vuông.
Giải thích: Hình thoi có bốn cạnh bằng nhau, khi xuất hiện thêm một góc vuông thì đồng thời các góc khác cũng vuông, nên hình đó thỏa mãn cả hai điều kiện của hình vuông.
Ví dụ: Trong hình thoi MNPQ, nếu góc ∠ M=90° , thì MNPQ là hình vuông.
Hình thoi có hai đường chéo bằng nhau
Nếu một hình thoi có hai đường chéo bằng nhau, thì hình đó là hình vuông.
Giải thích: Hình thoi có hai đường chéo vuông góc, khi chúng lại bằng nhau thì hình vừa có tính chất của hình thoi, vừa có tính chất của hình chữ nhật, do đó là hình vuông.
Ví dụ: Trong hình thoi EFGH, nếu EG=FH, thì EFGH là hình vuông.
Hình chữ nhật có hai đường chéo vuông góc
Nếu một hình chữ nhật có hai đường chéo vuông góc, thì hình đó là hình vuông.
Giải thích: Hình chữ nhật vốn có bốn góc vuông và hai đường chéo bằng nhau; khi hai đường chéo lại vuông góc, hình đó đồng thời có đặc điểm của hình thoi, vì vậy là hình vuông.
Ví dụ: Trong hình chữ nhật KLMN, nếu KL ⊥ MN, thì KLMN là hình vuông.
Tứ giác có bốn cạnh bằng nhau và một góc vuông
Một tứ giác bất kỳ được gọi là hình vuông nếu nó có bốn cạnh bằng nhau và có ít nhất một góc vuông.
Giải thích: Khi đã có một góc vuông, ba góc còn lại cũng sẽ là góc vuông, vì vậy hình có đủ bốn góc vuông và bốn cạnh bằng nhau – đúng với định nghĩa hình vuông.
Tứ giác có hai đường chéo bằng nhau và vuông góc với nhau
Nếu một tứ giác có hai đường chéo bằng nhau, cắt nhau tại trung điểm và vuông góc với nhau, thì đó chính là hình vuông.
Giải thích: Hai đường chéo vuông góc là đặc trưng của hình thoi, còn việc chúng bằng nhau là đặc trưng của hình chữ nhật. Kết hợp hai tính chất này, ta xác định được đó là hình vuông.
Tóm lại, có nhiều cách để nhận biết hình vuông, nhưng những dấu hiệu phổ biến và dễ áp dụng nhất gồm:
- Hình chữ nhật có hai cạnh kề bằng nhau.
- Hình thoi có một góc vuông hoặc hai đường chéo bằng nhau.
- Tứ giác có bốn cạnh bằng nhau và một góc vuông.
- Tứ giác có hai đường chéo bằng nhau và vuông góc tại trung điểm.
Việc nắm vững các dấu hiệu này giúp học sinh dễ dàng nhận biết và chứng minh một tứ giác là hình vuông trong các bài toán hình học, đồng thời hiểu rõ hơn mối quan hệ giữa các loại tứ giác đặc biệt như hình thoi, hình chữ nhật và hình vuông.
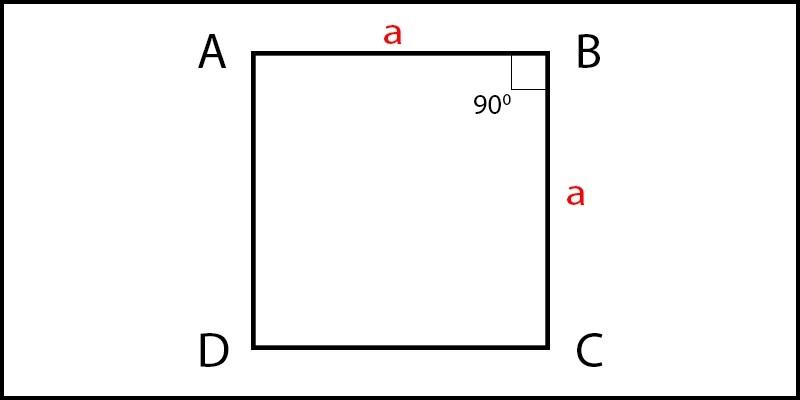
Các dạng bài tập về nhận biết hình vuông Để vận dụng các dấu hiệu để nhận biết hình vuông, học sinh cần làm quen với nhiều dạng bài tập khác nhau. Dưới đây là một số dạng phổ biến và lời giải chi tiết giúp bạn dễ hiểu, dễ áp dụng.
Dạng 1: Dựa vào hình chữ nhật có hai cạnh kề bằng nhau
Bài tập: Cho hình chữ nhật ABCD có AB=AD. Chứng minh rằng ABCD là hình vuông.
Lời giải:
Ta có: Hình chữ nhật ABCD có ∠ A=90∘ (theo tính chất hình chữ nhật).
Giả sử AB=AD, tức là hai cạnh kề bằng nhau.
Vậy hình chữ nhật có hai cạnh kề bằng nhau nên ABCD là hình vuông.
Kết luận: ABCD là hình vuông.
Dạng 2: Dựa vào hình thoi có một góc vuông
Bài tập: Cho hình thoi MNPQ có ∠ M=90∘. Chứng minh rằng MNPQ là hình vuông.
Lời giải:
Hình thoi MNPQ có bốn cạnh bằng nhau theo định nghĩa hình thoi.
Lại có một góc ∠ M=90∘.
Hình thoi có một góc vuông thì bốn góc đều vuông.
⇒ MNPQ là hình vuông.
Kết luận: MNPQ là hình vuông.
Dạng 3: Dựa vào hình thoi có hai đường chéo bằng nhau
Bài tập: Cho hình thoi EFGH có hai đường chéo EG và FHbằng nhau. Chứng minh rằng EFGH là hình vuông.
Lời giải:
Trong hình thoi, hai đường chéo luôn vuông góc nhau tại trung điểm.
Giả sử EG=FH, tức là hai đường chéo bằng nhau.
Hình thoi có hai đường chéo bằng nhau thì là hình vuông.
⇒ EFGH là hình vuông.
Kết luận: EFGH là hình vuông.
Dạng 4: Dựa vào tứ giác có bốn cạnh bằng nhau và một góc vuông
Bài tập: Cho tứ giác KLMN có KL=LM=MN=NK và ∠ K=90∘. Chứng minh KLMN là hình vuông.
Lời giải:
Tứ giác KLMN có bốn cạnh bằng nhau nên là hình thoi.
Trong hình thoi, nếu có một góc vuông thì là hình vuông.
⇒ KLMN là hình vuông.
Kết luận: KLMN là hình vuông.
Dạng 5: Dựa vào tứ giác có hai đường chéo bằng nhau và vuông góc
Bài tập: Cho tứ giác ABCD có hai đường chéo AC và BD bằng nhau, cắt nhau tại trung điểm O và AC⊥ BD. Chứng minh ABCD là hình vuông.
Lời giải:
Hai đường chéo vuông góc với nhau ⇒ ABCD có tính chất của hình thoi.
Hai đường chéo bằng nhau ⇒ ABCD có tính chất của hình chữ nhật.
Hình vừa là hình thoi vừa là hình chữ nhật ⇒ là hình vuông.
Kết luận: ABCD là hình vuông.
Dạng 6: Bài tập tổng hợp
Bài tập: Cho hình chữ nhật PQRS có PR và QS là hai đường chéo cắt nhau tại O, biết PR=QS và PR⊥ QS. Hỏi PQRS là hình gì?
Lời giải:
Hình chữ nhật có hai đường chéo bằng nhau (đúng theo tính chất).
Lại có hai đường chéo vuông góc với nhau.
⇒ Hình chữ nhật có hai đường chéo vuông góc là hình vuông.
Kết luận: PQRS là hình vuông.
💡 Tổng kết
Các bài tập nhận biết hình vuông thường xoay quanh các dấu hiệu cơ bản:
Hình chữ nhật có hai cạnh kề bằng nhau hoặc hai đường chéo vuông góc.
Hình thoi có một góc vuông hoặc hai đường chéo bằng nhau.
Tứ giác có bốn cạnh bằng nhau và một góc vuông.
Việc nắm vững và luyện tập thường xuyên các dạng bài này giúp học sinh hiểu rõ mối liên hệ giữa các tứ giác đặc biệt, đồng thời nhận biết và chứng minh hình vuông chính xác, nhanh chóng.
Trên đây, chúng tôi đã tổng hợp chi tiết về dấu hiệu nhận biết hình vuông, bao gồm các cách phân biệt, tính chất và bài tập minh họa giúp bạn hiểu rõ hơn về loại tứ giác đặc biệt này. Hy vọng bài viết sẽ giúp bạn dễ dàng áp dụng kiến thức để nhận biết và chứng minh hình vuông trong học tập cũng như trong thực tế đời sống.>> Tham khảo: Công thức tính công suất