Dấu hiệu nhận biết hình vuông
Hình vuông là một tứ giác đặc biệt có bốn cạnh bằng nhau và bốn góc vuông (mỗi góc 90° ). Đây là một trường hợp đặc biệt của hình chữ nhật vì có bốn góc vuông và đồng thời là hình thoi vì có bốn cạnh bằng nhau.
Những đặc điểm cơ bản của hình vuông:
- Cạnh: Bốn cạnh bằng nhau.
- Góc: Bốn góc đều bằng 90° , tức là vuông góc.
- Đường chéo: Hai đường chéo bằng nhau, giao nhau tại trung điểm mỗi đường, vuông góc với nhau và chia hình vuông thành bốn tam giác vuông cân bằng nhau.
- Đối xứng: Hình vuông có bốn trục đối xứng (hai đường chéo và hai đường trung trực của các cạnh) và tâm đối xứng tại giao điểm hai đường chéo.
- Chu vi và diện tích: Chu vi bằng cạnh nhân 4; diện tích bằng cạnh nhân cạnh.
Hình vuông không chỉ là một hình học cơ bản trong toán học mà còn được ứng dụng rộng rãi trong kiến trúc, thiết kế và đời sống hàng ngày, nhờ tính cân đối, đối xứng và dễ tính toán.
 Hình vuông là gì và có những đặc điểm gì?
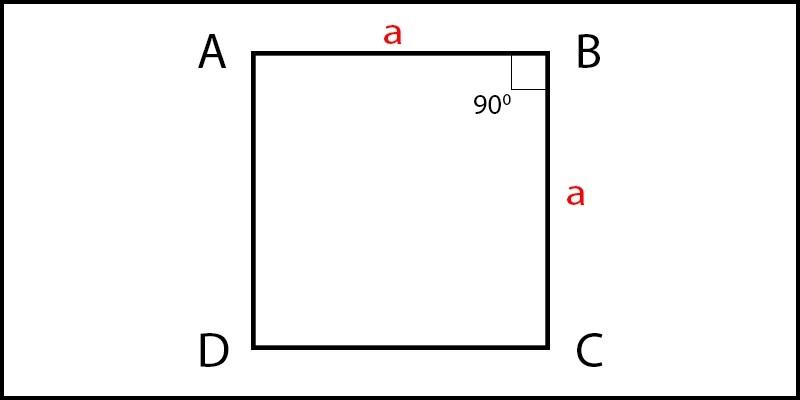
Hình vuông là gì và có những đặc điểm gì?Hình vuông là tứ giác có bốn cạnh bằng nhau, do đó các công thức tính chu vi và diện tích rất đơn giản:
Chu vi của hình vuông (P):
Chu vi bằng tổng độ dài bốn cạnh, tức:
P=4× a
Trong đó, aaa là độ dài một cạnh của hình vuông.
Diện tích của hình vuông (S):
Diện tích bằng cạnh nhân với chính nó, tức:
S=a× a=a²
Nhờ những công thức này, việc tính toán các đại lượng của hình vuông trở nên dễ dàng và nhanh chóng, đồng thời ứng dụng trong bài toán hình học, kiến trúc, thiết kế và đời sống hằng ngày.
 Hình vuông có những tính chất đặc biệt nào
Hình vuông có những tính chất đặc biệt nàoHình vuông không chỉ là một tứ giác có bốn cạnh bằng nhau và bốn góc vuông, mà còn sở hữu nhiều tính chất đặc biệt khiến nó trở thành hình học quan trọng trong toán học và ứng dụng thực tế.
Các tính chất đặc biệt của hình vuông:
Cạnh: Bốn cạnh bằng nhau.
Góc: Bốn góc đều bằng 90° (vuông góc).
Đường chéo:
Hai đường chéo bằng nhau và cắt nhau tại trung điểm.
Giao nhau vuông góc (tạo thành 4 tam giác vuông cân).
Chia hình vuông thành hai hình tam giác cân hoặc tứ giác nhỏ bằng nhau.
Đối xứng:
Có bốn trục đối xứng (hai đường chéo và hai đường trung trực của các cạnh).
Có tâm đối xứng tại giao điểm của hai đường chéo.
Quan hệ với hình khác:
Là hình chữ nhật đặc biệt (bốn góc vuông).
Là hình thoi đặc biệt (bốn cạnh bằng nhau).
Chu vi và diện tích:
Chu vi=4 × cạnh
Diện tích=cạnh × cạnh (a² )
Nhờ những tính chất này, hình vuông thường được sử dụng trong vẽ hình học, thiết kế kiến trúc, bố cục, và các bài toán tính toán hình học.
Hình vuông là một tứ giác đặc biệt, vì vậy có nhiều cách để nhận biết một hình là hình vuông dựa trên các đặc điểm về cạnh, góc và đường chéo. Việc nắm vững những dấu hiệu này không chỉ giúp giải các bài tập hình học dễ dàng hơn mà còn hỗ trợ trong các ứng dụng thực tế như kiến trúc, thiết kế hay bố trí vật thể.
Một số dấu hiệu phổ biến để nhận biết hình vuông bao gồm:
- Bốn cạnh bằng nhau và bốn góc vuông: Đây là dấu hiệu cơ bản và dễ nhận biết nhất. Nếu một tứ giác có tất cả các cạnh bằng nhau và mỗi góc đều 90° , chắc chắn đó là hình vuông.
- Hình chữ nhật có hai cạnh kề bằng nhau: Nếu một hình chữ nhật có hai cạnh kề bằng nhau, tức là bốn cạnh đều bằng nhau, khi đó hình chữ nhật này trở thành hình vuông.
- Hình thoi có một góc vuông: Một hình thoi thường có bốn cạnh bằng nhau nhưng không nhất thiết các góc vuông. Tuy nhiên, nếu có ít nhất một góc vuông, thì hình thoi đó chính là hình vuông.
- Đường chéo vuông góc và bằng nhau: Nếu hai đường chéo của tứ giác cắt nhau tại trung điểm, vuông góc với nhau và bằng nhau về độ dài, tứ giác đó là hình vuông. Đây là một dấu hiệu nhận biết rất đặc trưng, nhất là trong các bài toán nâng cao.
- Đường chéo chia tứ giác thành bốn tam giác vuông cân bằng nhau: Khi hai đường chéo cắt nhau, chúng tạo thành bốn tam giác vuông cân, một đặc điểm duy nhất của hình vuông so với các tứ giác khác.
Những dấu hiệu nhận biết hình vuông này giúp người học nhanh chóng phân biệt hình vuông với hình chữ nhật, hình thoi hay các tứ giác khác, đồng thời là cơ sở để tính toán chu vi, diện tích, vẽ hình và áp dụng vào các bài toán thực tế. Nắm vững các dấu hiệu này sẽ giúp việc học hình học trở nên dễ dàng và trực quan hơn, đồng thời hiểu rõ hơn về các tính chất đặc biệt mà chỉ hình vuông mới có.
 Ứng dụng của hình vuông trong đời sống và kiến trúc
Ứng dụng của hình vuông trong đời sống và kiến trúcHình vuông không chỉ là một khái niệm cơ bản trong toán học mà còn được ứng dụng rộng rãi trong đời sống hàng ngày, thiết kế và kiến trúc, nhờ đặc tính cân đối, đối xứng và dễ tính toán.
Trong đời sống hàng ngày:
Đồ vật hàng ngày: Nhiều vật dụng như bàn, ghế, gạch lát sàn, khăn trải bàn hay các đồ hộp thường có hình vuông vì dễ bố trí, sắp xếp và tạo cảm giác cân đối.
Học tập và trò chơi: Hình vuông xuất hiện trong các bài tập hình học, trò chơi cờ vua, bàn cờ caro, giúp trẻ nhận biết về các hình khối và rèn luyện tư duy không gian.
Trong kiến trúc và thiết kế:
Thiết kế công trình: Hình vuông được sử dụng trong bố cục phòng ốc, nền nhà, cửa sổ hay sân vườn để tạo sự cân đối, hài hòa và dễ đo đạc.
Trang trí nội thất: Các hoa văn, gạch lát, trần nhà hay ô cửa sổ hình vuông tạo nên vẻ đẹp đối xứng, hiện đại và dễ phối hợp với các hình học khác.
Quy hoạch đô thị: Trong quy hoạch các khu dân cư hay công viên, các ô đất hình vuông giúp dễ phân lô, xây dựng và tối ưu không gian.
Nhờ những ứng dụng này, hình vuông trở thành hình khối quen thuộc và hữu ích trong cả đời sống thường nhật lẫn thiết kế kiến trúc, vừa đảm bảo tính thẩm mỹ, vừa thuận tiện cho việc đo đạc, sắp xếp và thiết kế không gian.
Trên đây chúng tôi đã tổng hợp chi tiết các dấu hiệu nhận biết hình vuông, từ khái niệm, tính chất đặc biệt, công thức tính chu vi – diện tích đến các ứng dụng trong đời sống và kiến trúc. Hy vọng bài viết dấu hiệu nhận biết hình vuông sẽ giúp bạn đọc nắm vững kiến thức cơ bản về hình vuông, nhận biết và phân biệt hình vuông với các tứ giác khác một cách dễ dàng.